Opera Funktionen
Optimierte Arbeitsabläufe für die Simulation von magnetischen Systemen, Elektromotoren und anderen elektrische Maschinen
Opera Funktionen für niederfrequente Elektromagnetik
Opera stellt den Benutzern eine intuitive grafische Benutzeroberfläche (GUI) zur Verfügung, um parametrisierte Modelle zu erstellen oder Komponenten oder Baugruppen aus einem CAD-System zu verwenden. Die integrierten Nachbearbeitungsfunktionen ermöglichen den Zugriff auf die Simulationsergebnisse. Opera erleichtert die Simulation von Maschinen in dedizierten Umgebungen. Dabei können typische Materialeigenschaften und der Einfluss anderer physikalischer Bereiche auf die Geräteleistung berücksichtigt werden. Die automatische Optimierung unterstützt den Erfolg der Konstruktion.
- Grafische Benutzeroberfläche
- Anwendungsumgebungen
- Materialien
- Multiphysik
- Optimierung
Grafische Benutzeroberfläche von Opera
Komponenten oder Baugruppen können aus einem vorhandenen CAD-System importiert oder mit dem integrierten Opera 2D-Skizzierer oder 3D Modeler erstellt werden. Die Opera Modelldatei enthält einen vollständigen Verlauf der Befehle, die zur Erstellung genutzt wurden. Der Anwender kann Dateien wiedergeben und ändern, indem er die Dateien als Vorlage verwendet, um die Konstruktionsvarianten von Standardprodukten zu automatisieren.
Zu den Funktionen bei der Vorverarbeitung gehören:
- CAD-Import
- Geometriekonstruktion (boolesche Operationen, Translationsflächen, Ausformung zwischen Flächen, 2D-Skizzen, Kopieren und Transformieren, Hintergrundbereich, Verrundung und Fase)
- Parametrierung und Wiederaufbau
- Automatische Vernetzung (Netzsteuerung, Schichtung für Skin-Effekt und dünne Bleche)
- Definition externer Schaltkreise
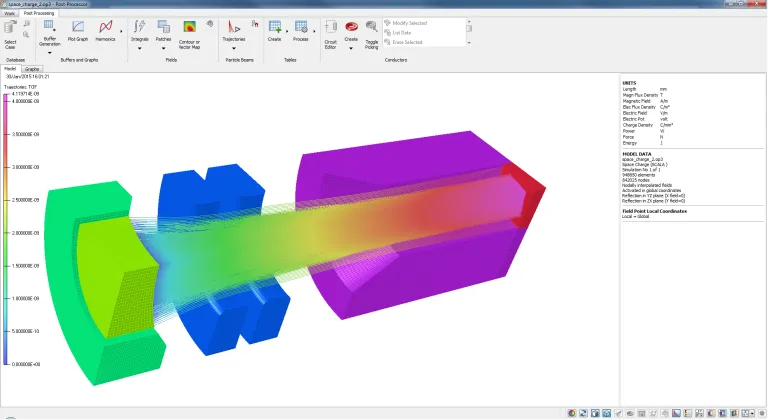
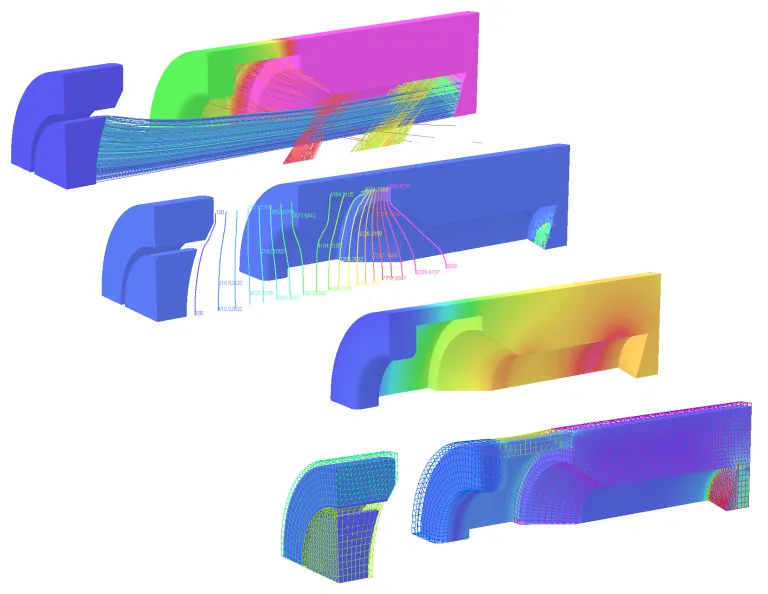
Nach Abschluss der Simulation vereinfacht der Opera Postprozessor die Analyse der Ergebnisse. Neben der Anzeige des Feldes, der Temperatur oder der Belastung gibt es zahlreiche Funktionen zum Vorbereiten und Anzeigen abgeleiteter Quantitäten in den dem Anwender bekannten Formularen und Einheiten. Dazu gehören Kräfte, Leistungsverluste und gespeicherte Energie. Darüber hinaus kann der Anwender auch Teilchenbahnen über die berechneten elektrischen und magnetischen Felder berechnen und anzeigen.
Die Nachbearbeitungsfunktionen umfassen:
- Feldwerte:
- Konturen und Vektoren auf 3D-Geometrieoberflächen
- Konturen und Vektoren auf beliebigen planaren, zylindrischen und sphärischen 2D-Oberflächen
- Diagramme entlang Linien, Kreisen und Bögen im 3D-Raum
- Isoflächen
- Export in Textdateien
- Integrierte Werte (Kraft- und Drehmoment, Energie und Leistung, Linien-, Oberflächen- und Volumenintegrale, Q-Faktor)
- Harmonische Analyse
- Verformte Formen
- Verfolgung geladener Teilchen (Anzeige in Geometrie, Schnittpunkt mit Oberflächen, Karten zur Strahlstromdichte)
Opera Anwendungsumgebungen
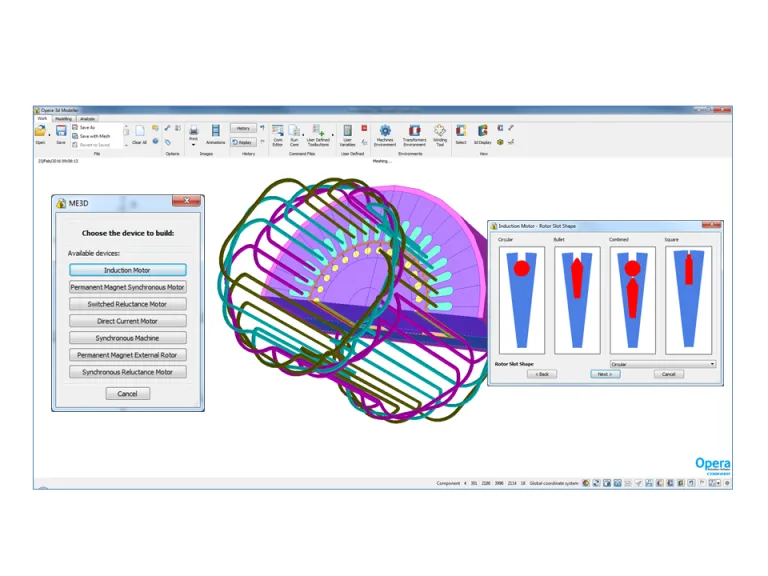
Die Maschinenumgebung unterstützt die schnelle Einrichtung von Motor- und Generatormodellen und deren Analyse mit parametrisierten Vorlagen. Die Maschinenumgebungen ermöglichen eine umfassende Modellanpassung, um die Designanforderungen des Anwenders zu erfüllen.
Zu den verfügbaren Standardmaschinen gehören:
- DC-Maschinen
- Induktionsmaschinen
- Permanentmagnet-Synchronmaschinen
- Permanentmagnet-Außenrotor-Maschinen
- Geschalteter Reluktanzmotor
- Synchroner Reluktanzmotor
- Synchrone Maschine
Opera kann standardmäßige Konstruktionsberechnungen durchführen, um nützliche Ergebnisse wie rückwirkende EMK, Rastmoment, Lastmoment, Leerlauf- und Kurzschlusskurven zu erhalten.
Eine direkte Kopplung mit dem Opera Optimizer ermöglicht die Verfeinerung und Optimierung von Konstruktionen auf Grundlage der Benutzeranforderungen.
Die Transformatorumgebung ermöglicht die automatische Definition von Transformator- und Reaktormodellen sowie die Lösung und Vorbereitung für die Optimierung. Zu den Standardanalysen gehören Kurzschluss, Open Circuit und Einschaltstrom. Opera führt eine Finite-Element-Analyse durch, was bedeutet, dass die Ergebnisse anhand von echten nichtlinearen Eigenschaften und repräsentativen Steuerkreise berechnet werden. Zu den automatischen Ausgabegrößen gehören Impedanzen, Widerstände, Kräfte und Verluste sowie die üblichen Anzeigeoptionen für die magnetische Flussdichte und andere Größen. Durch die Integration der Transformatorumgebung in den Opera Optimierer kann der Anwender automatisch Parameter wie Kernabmessungen durch Schraubendurchmesser optimieren.
Die Standardergebnisse der Transformatorumgebung umfassen:
- Effizienz
- Induktivitäten
- Sättigungskurven
- Kurzschlussanalyse
- Analyse offener Schaltungen
- Einschaltstrom/Lasttests
- Einschalttransienten
- Verluste – Kupfer, Wirbelstrom, Hysterese
- Konstruktionsoptimierung
- Co-Simulation mit Simulink®
- Streufeld-/Abschirmungsanalyse (EMV/EMI)
- Dynamische Kräfte auf Spulen
Materialeigenschaften in Opera
Es gibt Lösungsoptionen für Materialien, die Folgendes aufweisen:
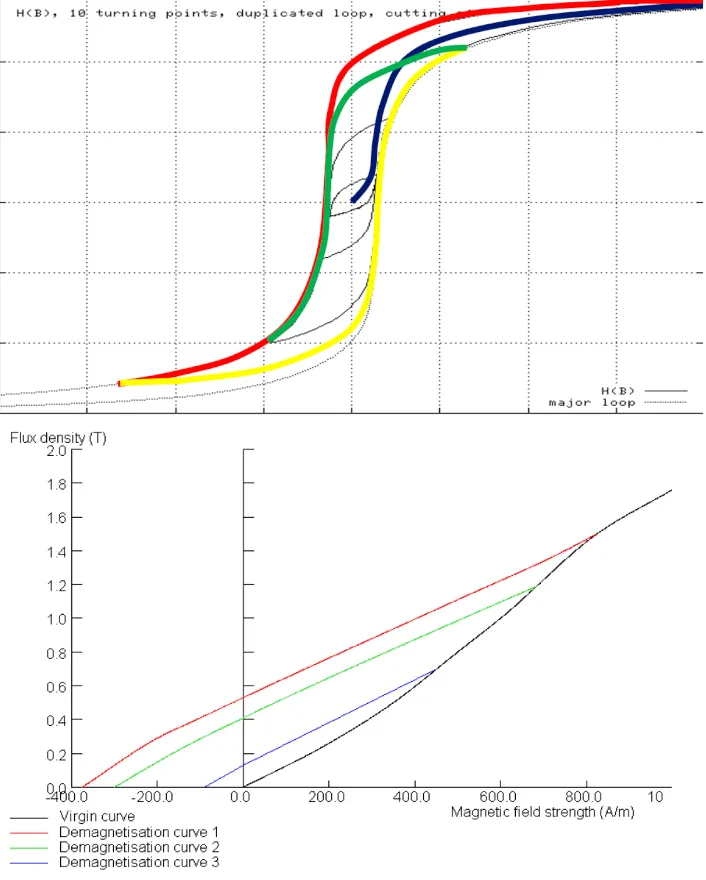
- Lineares oder nichtlineares elektromagnetisches Verhalten (mit Hysterese)
- Isotrope, orthotrope oder laminierte Eigenschaften
- Eigenschaften von Permanentmagneten (einschließlich Magnetisierungs- und Entmagnetisierungslösungen)
Opera Multiphysik-Simulation
Opera hilft bei der Konstruktion elektromagnetischer/elektromechanischer Geräte. Daher ist der Funktionsumfang der Software vor allem auf die Niederfrequenz-Elektromagnetik ausgerichtet. Sie enthält jedoch auch andere physikalische Funktionen, wie z. B. strukturelle Spannungen und thermische Analysen, als Unterstützungsfunktionen. Opera ist also eine multiphysikalische Software. Analysen sind verkettet. Ergebnisse werden zwischen den verschiedenen physikalischen Bereichen übergeben. Eigenschaften sind nichtlinear. Der Anwender kann beispielsweise eine elektromagnetische Analyse durchführen und an eine thermische Analyse übergeben, die Wärmeverteilung berechnen und anschließend eine elektromagnetische Analyse unter Berücksichtigung der temperaturabhängigen Materialeigenschaften durchführen. Opera ermöglicht so Untersuchungen wie Drehmomentverlust bei Permanentmagnetmotoren oder Homogenitätsstudien bei Magneten unter Last.
Optimierung mit Opera
Der Opera Optimizer ist ein Softwaretool, das Anwender beim Erreichen optimaler Designs unterstützt. Die vollständige Integration in Opera ermöglicht eine schnelle und einfache Untersuchung möglicher Konstruktionsräume für Multiphysik-Probleme. Dabei wird ein effizienter Optimierungsalgorithmus unter Kombination deterministischer und stochastischer Methoden verwendet, um Optimierungsprobleme für einzelne oder mehreren Zielen zu lösen.
Optimierungsproblemdefinition mit:
- Konstruktionsvariablen und numerischen Grenzwerten
- Ungleichheits- und Gleichheitsbedingungen
- Zielfunktionen zur Minimierung oder Maximierung
Optimierung der Prozesssteuerung durch:
- Abbruchkriterien für den Optimierungsalgorithmus
- Gestaltung der anfänglichen Populationsverteilung
- Auswahl beizubehaltender Lösungsdatenbanken
Mehr erfahren
Erfahren Sie, was SIMULIA für Sie tun kann
Lassen Sie sich von unseren SIMULIA Experten zeigen, wie unsere Lösungen eine nahtlose Zusammenarbeit und nachhaltige Innovation in Unternehmen jeder Größe ermöglichen.
Erste Schritte
Wir bieten Kurse und Schulungen für Studenten, Hochschulen, Fachleute und Unternehmen an. Finden Sie die passende SIMULIA Schulung.
Hilfe anfordern
Informationen zu Software- und Hardware-Zertifizierungen, Software-Downloads, Anwenderdokumentation, Support-Kontakten und Serviceangeboten finden