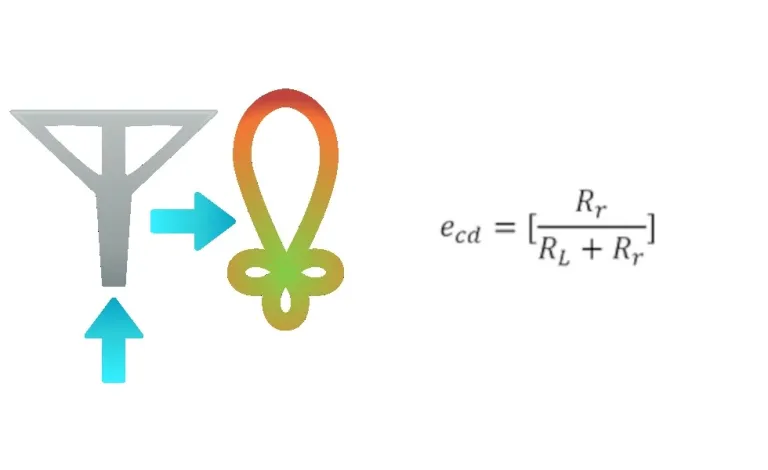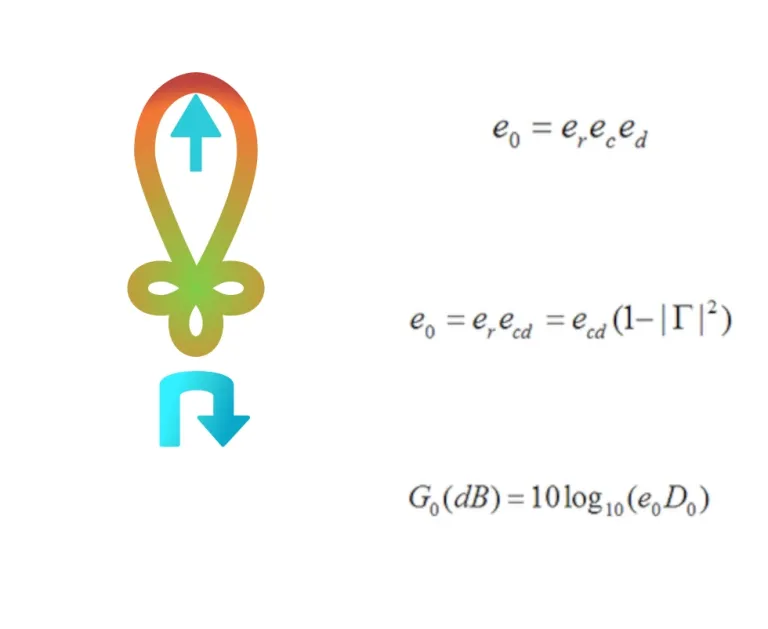Antenna Magus Rechner
Antenna Magus Toolbox für die vereinfachte Antennenkonstruktion
Die Antenna Magus Toolbox
Die Antenna Magus Toolbox enthält eine Reihe nützlicher Tools und Dienstprogramme für Antennenkonstrukteure zur Vereinfachung alltäglicher Aufgaben im Bereich der Antennenentwicklung. Wir gruppieren diese Werkzeuge nach Antenneneigenschaften, Systemrechnern, Näherungswerkzeugen, Datenumwandlungstools, allgemeinen Eigenschaften und Übertragungsleitungsrechnern.
- Datenkonvertierung
- Systemrechner
- Übertragungsleitungsrechner
- Antenneneigenschaften
- Reflektoren
- Allgemeine Eigenschaften
Chart Tracing Tool
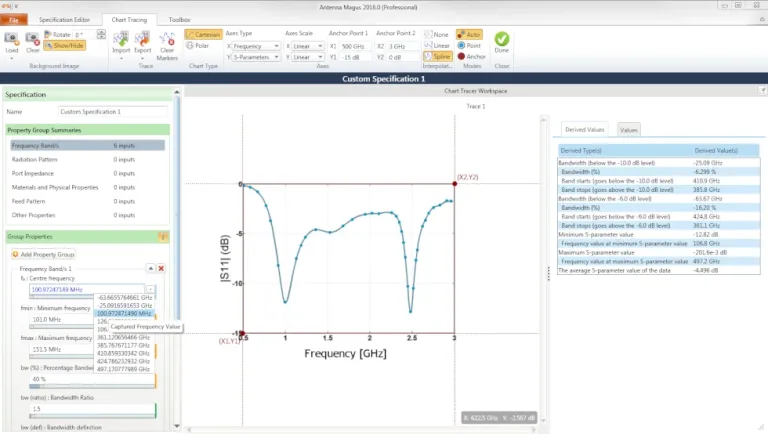
Das Chart Tracing Tool ist wahrscheinlich eines der nützlichsten Dienstprogramme in Antenna Magus. Es begann als interne Anwendung, die von den Ingenieuren zum Auslesen von Konstruktionswerten aus gescannten Diagrammen verwendet wurde, hauptsächlich aus veröffentlichten Artikeln, die nur als PDF oder in Papierform verfügbar waren. Nachdem wir das Werkzeug anderen Ingenieuren gezeigt und deren Begeisterung gesehen haben, entschieden wir uns, es als ein Dienstprogramm in Antenna Magus aufzunehmen.
Wählen Sie einfach Ihr gescanntes Diagrammbild aus, legen Sie Ankerwerte fest und folgen Sie den Kurven mit der Maus. Wenden Sie den Spline oder die lineare Funktion an, und exportieren Sie die XY-Werte in eine TSV-Datei (Tab Separated Values). Es unterstützt sowohl polare als auch kartesische Diagramme.
Das Chart Tracing Tool extrahiert automatisch Werte, die für den angegebenen Datentyp relevant sind, und erleichtert so die Bestimmung von Größen der Daten wie Bandbreite, Nebenkeulenebene usw. Sie können diese Werte für die Verfeinerung von Konstruktionen oder Spezifikationen verwenden.
Lesen Sie mehr über die Verwendung des Chart Tracing Tool.
Angle Conversion Calculator
Dieser Rechner konvertiert Winkelwerte zwischen verschiedenen Einheitentypen. Die Tabelle zeigt die Faktoren, die zur Umrechnung in Grad verwendet werden.
| Konvertieren von | Multiplikationsfaktor |
| Grad | 1 |
| Radiant | 180/π |
| Gon grade | 360/400 |
| Minuten | 1/60 |
| Sekunden | 1/3600 |
| Milliradiant | 180/(1000*π) |
| Rotation | 360 |
Length Unit Conversion Tool
Dieser Rechner konvertiert Längenwerte zwischen verschiedenen Einheitentypen. Die Tabelle zeigt die Faktoren, die zur Umrechnung in Meter verwendet werden.
| Konvertieren von | Multiplikationsfaktor |
| Mikrometer | 1e-6 |
| Mikrometer | 1e-6 |
| Millimeter | 1e-3 |
| Zentimeter | 1e-2 |
| Meter | 1 |
| Kilometer | 1e3 |
| Millizoll | 25,4e-6 |
| Zoll | 25,4e-3 |
| Fuß | 0,3048 |
| Yard | 0,9144 |
| Meile | 1609,344 |
dB-V-P Ratio Tool
Die Gleichung zeigt das Verhältnis zwischen einem Dezibelwert und einem linearen Spannungs-/Leistungsverhältnis. Sie können diesen Rechner auf drei Arten verwenden:
- Geben Sie Dezibelwerte an und der Rechner gibt die linearen Spannungs- und Leistungsverhältnisse zurück.
- Geben Sie ein lineares Spannungsverhältnis an und der Rechner gibt den Dezibelwert zusammen mit dem linearen Leistungsverhältnis zurück.
- Geben Sie ein lineares Leistungsverhältnis an und der Rechner gibt den Dezibelwert zusammen mit dem linearen Spannungsverhältnis zurück.
dB = 20log10 (Spannungsverhältnis) = 10log10 (Leistungsverhältnis)
Two-Port Network Conversion Tool
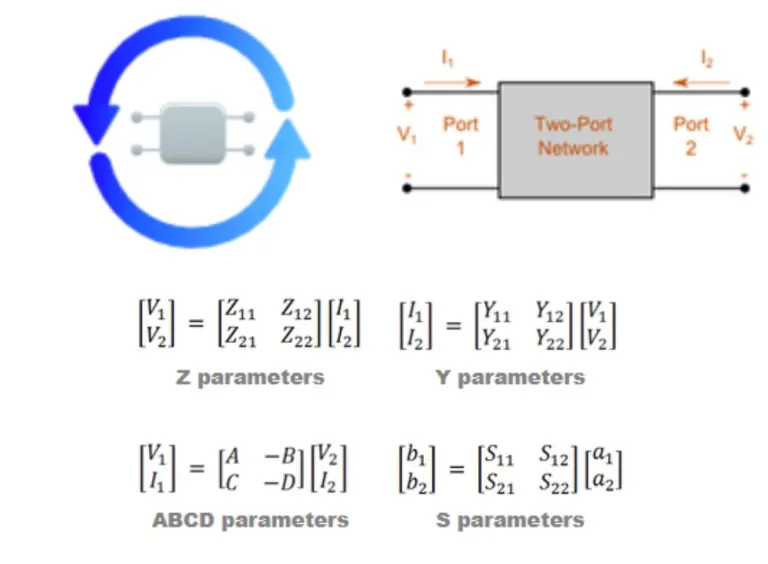
Dieser Rechner ermöglicht die Konvertierung zwischen verschiedenen Zwei-Port-Parametern. Zu den Zwei-Port-Parametern gehören Z (Impedanz-Matrix), Y (Admittanz-Matrix), ABCD-Parameter (Kettenmatrix) und S-Parameter (Streuparameter).
Die meisten Mikrowellen-Lehrbücher [z. B. Pozar] bieten nützliche Umwandlungsformeln zum Wechsel zwischen verschiedenen Zwei-Port-Parameterkonventionen. Die Bücher bieten jedoch oft nur Konvertierungen für vereinfachte Fälle. Dies gilt insbesondere dann, wenn die Impedanzwerte von Port 1 (Quelle) und Port 2 (Last) reell oder gleich sind oder wenn ein gemeinsamer Port und die Systemimpedanz erzwungen werden.
Mit diesem Rechner kann die Impedanz der beiden Ports anhand der von Dean Frickey entwickelten Gleichungen komplex und eindeutig sein. Die Abbildung zeigt ein Zwei-Port-Standardnetzwerk und grundlegende Zwei-Port-Gleichungen.
VSWR Return Loss Calculator
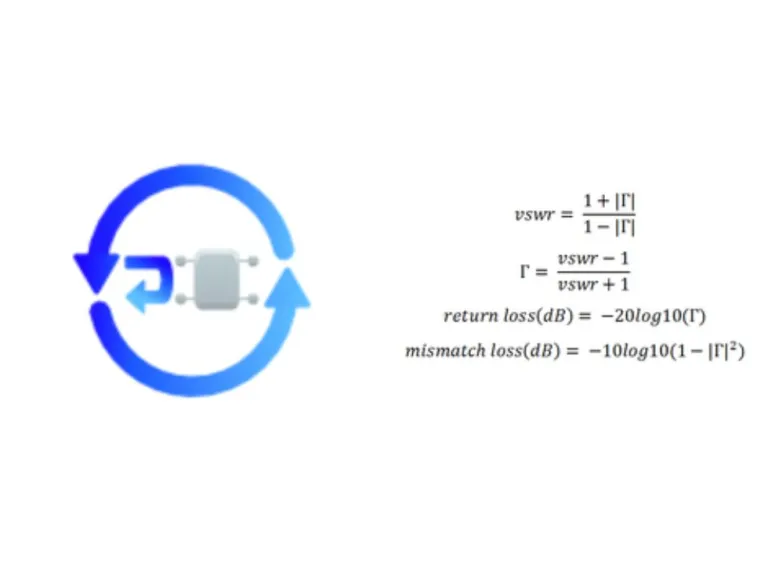
Das Stehwellenverhältnis(VSWR), der Reflexionskoeffizient (Τ), der Reflexionsverlust und der Fehlanpassungsverlust sind voneinander abhängig, wie wir anhand der Gleichungen sehen.
Dieser Rechner besteht aus vier Konstruktionsgruppen. Jede Gruppe benötigt eine Zieleingabe und gibt die verbleibenden drei zurück.
Friis Transmission Equation Calculator
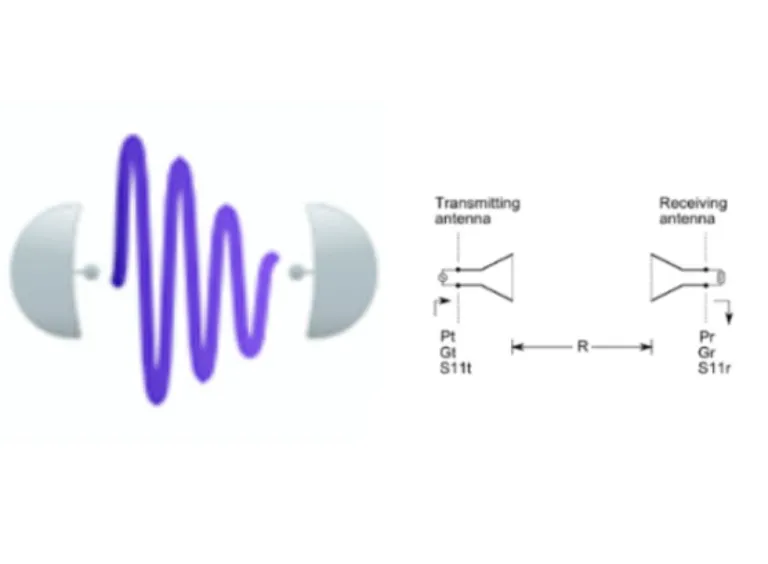
Dieser Rechner löst die Friis-Übertragungsgleichung für jede ihrer Variablen auf. Die Friis-Übertragungsgleichung setzt die von einer Antenne empfangene Leistung in Bezug zu der Leistung, die von einer anderen Antenne in einer bestimmten Entfernung (im freien Raum) abgestrahlt wird. Die geänderten Formen der Friis-Grundgleichung ermöglichen die Einbeziehung vieler Systemfaktoren, einschließlich Nichtübereinstimmung der Antenne, Absorption im Übertragungsmedium, Kabelverlust usw. Der Antenna Magus Rechner schließt Effekte der Antennenfehlanpassung mit ein. Er gleicht keine Polarisierung und physische Fehlausrichtung aus, kann sie jedoch durch Anpassung der für die Verstärkung der jeweiligen Antennen verwendeten Werte berücksichtigen.
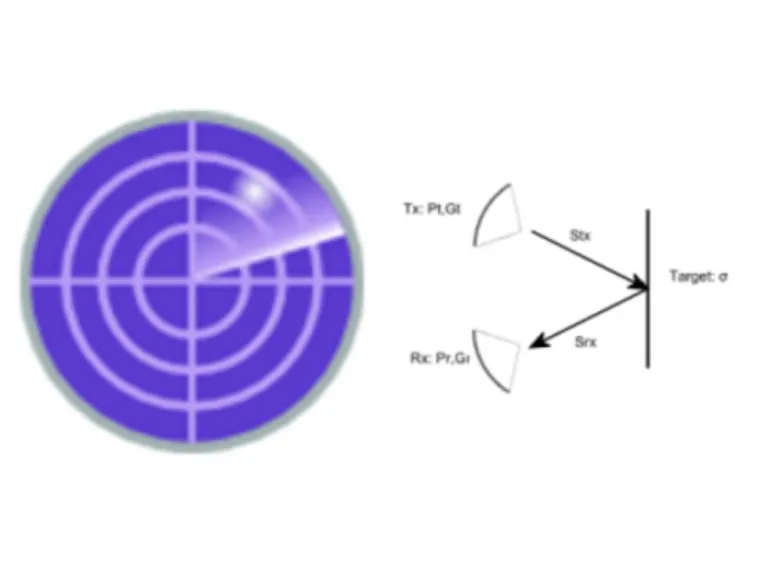
Radar Range Equation Tool
Dieser Rechner löst die bekannte Radarbereichsgleichung für jede ihrer Variablen auf. Die Gleichung für den Radarbereich setzt die vom Radarempfänger empfangene Leistung in Bezug zu:
- der vom Radarsender übertragenen Leistung,
- dem Radarquerschnitt des Ziels,
- der Verstärkung der Antennen,
- der Frequenz und
- dem Abstand zwischen den Antennen und dem Ziel.
Die Form der Gleichung, die in diesem Rechner verwendet wird, ermöglicht ein bistatisches Radar, berücksichtigt jedoch keine Polarisationsabweichung oder Verstärkungskompensation für falsch ausgerichtete Antennen.
Signal to Noise Ratio Tool
Das Signal-Rausch-Verhältnis (SNR) ist ein Kriterium der Nachweisbarkeit in einer Kommunikationsverbindung. Einfach ausgedrückt vergleicht es den Pegel des erforderlichen Signals mit dem Pegel des Hintergrundrauschens. Ein Verhältnis von mehr als 1:1 bedeutet mehr Signal als Rauschen.
Die in diesem Tool verwendete Gleichung ist hier dargestellt. Die in der Gleichung verwendeten Parameter sind:
- Sendeleistung (Pt),
- effektive Antennenfläche des Senders (Aet),
- effektive Antennenfläche des Empfängers (Aer),
- Sender-Empfänger-Abstand (r),
- Wellenlänge (λ),
- Bandbreite (B),
- Boltzmann-Konstante (k).
- Systemtemperatur
Die folgenden Eingabeparameter ergeben beispielsweise ein Signal-Rausch-Verhältnis (SNR) von 72,78e-3.
- Sendeleistung: 1 mW
- Betriebsfrequenz: 1 GHz
- Effektive Antennenfläche des Senders (AET): 78,53 cm2
- Effektive Antennenfläche des Empfängers (AER): 100 cm2
- Antennenabstand: 10 km
- Systembandbreite: 30 MHz
- Systemtemperatur: 290 K
Tool für passive Fernerkundung
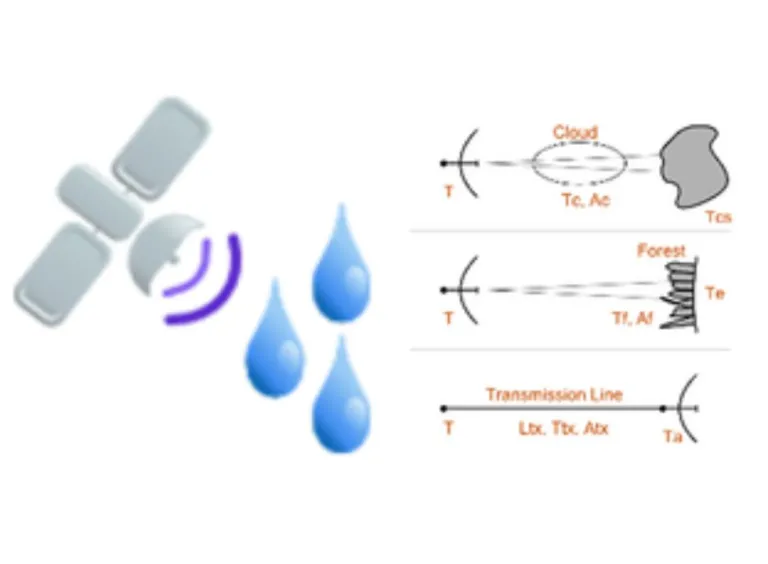
Radioteleskope sind Fernerkundungsgeräte. Erdbasierte Teleskope zeigen auf den Himmel, um himmlische Objekte zu beobachten. Teleskope, die auf Flugzeugen oder Satelliten installiert sind, zeigen auf die Erde. Die Gleichung setzt voraus, dass die vom Teleskop erkannte Strahlung in den beobachteten Objekten entsteht, was als passive Fernerkundung bezeichnet wird.
Dieses Tool berechnet die Temperatur (gemessen oder die des Objekts) für verschiedene Fernerkundungsanwendungen:
- Ein erdbasiertes Radioteleskop führt eine Fernerkundung von Himmelskörpern durch eine Gaswolke durch.
- Ein Radioteleskop auf einem Satelliten führt eine Fernerkundung der Erde durch Wald durch.
- Der Empfänger erkennt die Antennenleistung über die Übertragungsleitung.
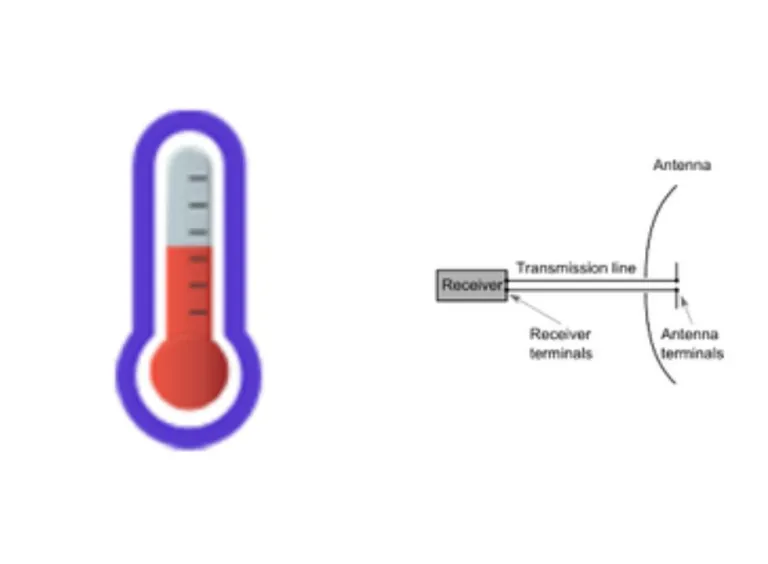
Systemtemperaturrechner
Die Antenne ist Teil des Empfangssystems und besteht im Allgemeinen aus einer Antenne, einem Empfänger und einer Übertragungsleitung, die diese verbindet. Die Temperatur des Systems ist ein kritischer Faktor bei der Bestimmung der Empfindlichkeit und des Signal-Rausch-Verhältnisses eines empfangenden Systems.
Die in diesem Tool verwendete Gleichung lautet:
Die in der Gleichung verwendeten Parameter sind:
- Antennenrauschtemperatur in Kelvin (Tan),
- physische Antennentemperatur in Kelvin (Tap),
- Antennenwirkungsgrad (Ea),
- physische Temperatur der Übertragungsleitung in Kelvin (Tlp),
- Übertragungsleitungseffizienz (El),
- Rauschtemperatur des Empfängers in Kelvin (Trn),
was eine Systemtemperatur in Kelvin (Tsys) ergibt.
Rechner für Kommunikations-Downlink
Ein Kommunikationssatellit fungiert als Funkrelais im Raum. Die Kommunikationsverbindung kann zwischen Stationen auf der Erde oder zwischen Antennen von anderen Satelliten bestehen.
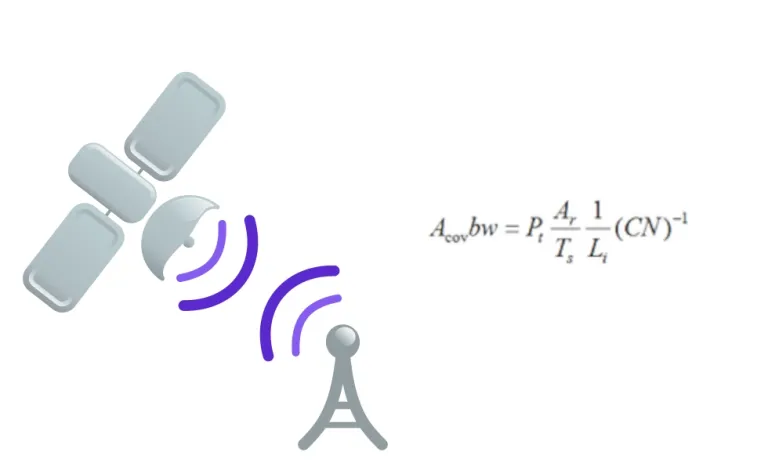
Eine Möglichkeit, die Kapazität des Systems zu erhöhen, ist die Erhöhung der Bandbreite (bw). Die Frequenzwiederverwendung ist eine Möglichkeit, die Bandbreite zu erhöhen. In Fällen mit einem festen Träger-Rausch-Leistungsverhältnis (CN) kann die Verringerung des Abdeckungsbereichs (Acov) die Bandbreite erhöhen. Mehrstrahlantennen können den Abdeckungsbereich reduzieren, da sie die Leistung auf die Strahlen aufteilen.
Weitere Parameter der Gleichung sind die Satellitensendeleistung (Pt), der effektive Bereich der Bodenstationsantenne (Ar), die äquivalente Systemtemperatur (Ts) und der zugehörige Verlust (Li).
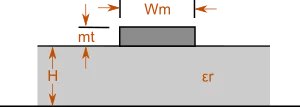
Mikrostreifenleitung
Dieser Rechner bestimmt die elektrischen Merkmale für die gegebenen physikalischen Eigenschaften einer Mikrostreifenleitung oder umgekehrt. Bei den Berechnungen wird die Auswirkung der Dicke der Metallisierung berücksichtigt.
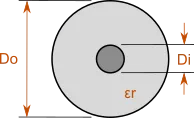
Koaxial Kabel
Dieser Rechner bestimmt die Impedanz für ein bestimmtes physisches Koaxial oder berechnet den Innen- oder Außendurchmesser für die angegebenen Parameter. Er berechnet auch andere Übertragungsleitungsparameter wie Kapazität und Induktivität pro Einheitslänge.
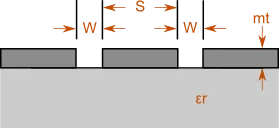
Koplanarer Wellenleiter
Dieser Rechner bestimmt die elektrischen Merkmale für die gegebenen physikalischen Eigenschaften einer koplanaren Wellenleiterstruktur oder umgekehrt. Bei den Berechnungen wird die Auswirkung der Metallisierungsdicke berücksichtigt.
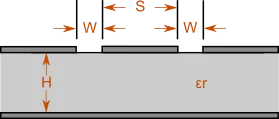
Geerdeter koplanarer Wellenleiter
Dieser Rechner bestimmt die Impedanz für die gegebenen physikalischen Eigenschaften einer geerdeten koplanaren Wellenleiterstruktur.
Rundhohlleiter
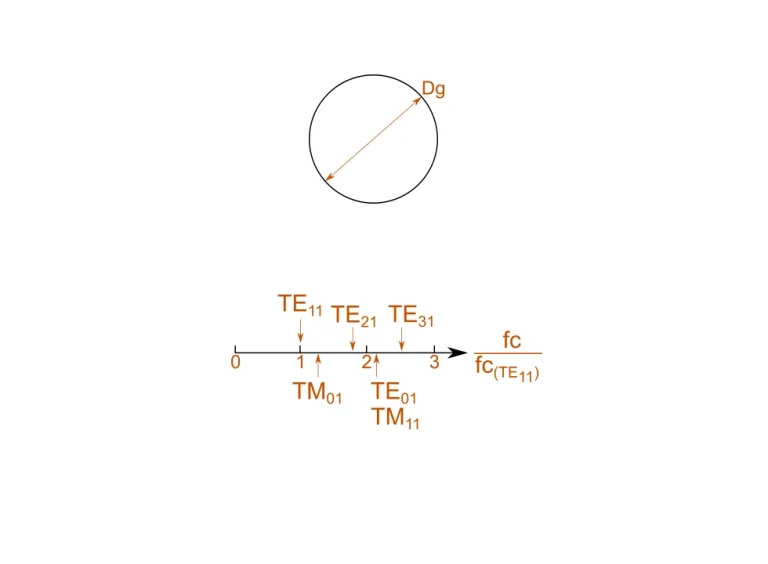
Dieser Rechner bestimmt die Grenzfrequenz, die Wellenimpedanz und die geführte Wellenlänge der ersten fünf dominanten Modi für den definierten kreisförmigen Wellenleiter.
Der Grundbetriebsmodus in einem kreisförmigen Wellenleiter ist der TE11-Modus. Wir zeigen eine Darstellung der relativen Grenzfrequenzen, wobei die Frequenzen auf die Grenzfrequenz des grundlegenden TE11-Modus normalisiert werden.
Rechteck-Hohlleiter
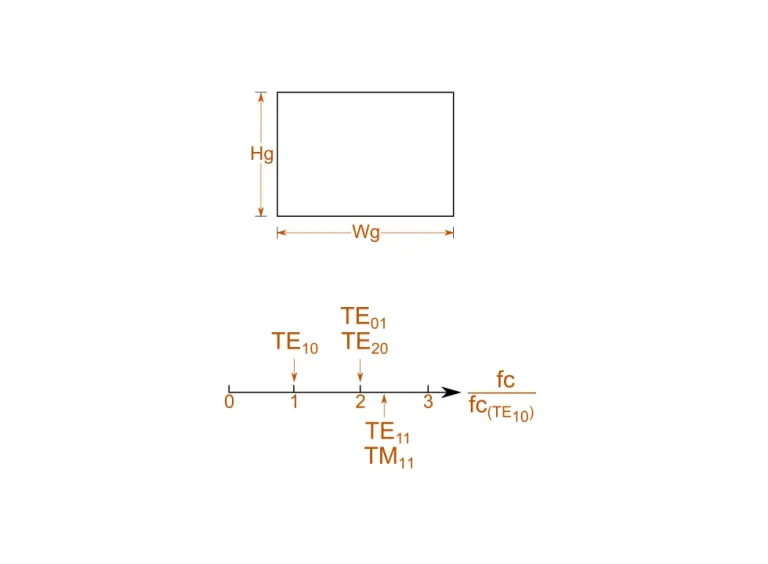
Dieser Rechner bestimmt die Grenzfrequenz, die Wellenimpedanz und die geführte Wellenlänge der ersten fünf dominanten Modi für den definierten rechteckigen Wellenleiter.
Der Grundbetriebsmodus in einem Rechteck-Hohlleiter ist der TE10-Modus. In diesem Modus hängt die Impedanz des Wellenleiters vollständig von der Breite des Wellenleiters ab. Wir zeigen eine Darstellung der relativen Grenzfrequenzen, wobei die Frequenzen auf die Grenzfrequenz des grundlegenden TE10-Modus normalisiert werden.
Gewinn-/Strahlbreiten-Umwandler
Dieser Rechner berechnet einen ungefähren Antennengewinn für vorgegebene Strahlbreiten oder umgekehrt. Der genaue Antennengewinn hängt von vielen Faktoren ab, aber dieser praktische Rechner bietet eine nützliche Faustregel. Der Rechner ermöglicht die separate Angabe der vertikalen und horizontalen Strahlbreite.
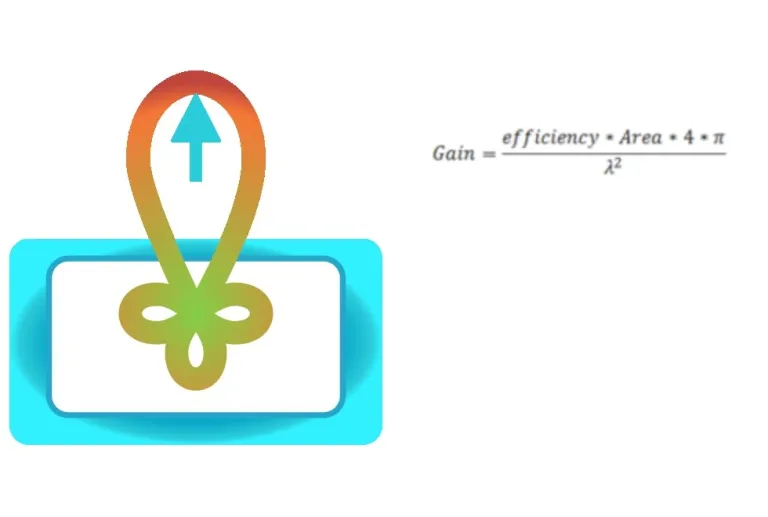
Antennengewinn aus Apertur
Dieser Rechner berechnet den erwarteten Antennengewinn für eine Apertur einer bestimmten Fläche und Effizienz. Er kann die Gleichung auch umkehren, um sie für einen der anderen Parameter zu lösen. So wird beispielsweise die Apertureffizienz einer Hornantenne berechnet.
Tool für den Antennenwirkungsgrad
Der Antennen-Gesamtwirkungsgrad berücksichtigt Verluste an den Eingängen und innerhalb der Struktur der Antenne. Typische Verluste sind:
- Reflexionen aufgrund der Fehlanpassung zwischen Übertragungsleitung und Antenne
- Verluste (Leitung und Dielektrikum)
Dieses Tool berechnet den Gesamtwirkungsgrad der Antenne mithilfe der folgenden Gleichung:
e0 = er ecd
dabei gilt
E0 = Gesamtwirkungsgrad der Antenne
Er = Reflexionseffizienz (Fehlanpassung) = (1 - |Τ|2)
Ecd = Strahlungseffizienz der Antenne
T = Reflexionsfaktor an den Eingangsklemmen der Antenne [Τ=(Zin- Z0)/( Zin- Z0), dabei gilt Zin = Antenneneingangsimpedanz, Z0 = charakteristische Impedanz der Übertragungsleitung].
Tool für den Antennenwirkungsgrad
Der Gesamtwirkungsgrad der Antenne berücksichtigt die Reflexions-, Leitungs- und dielektrischen Verluste einer Antenne. Die dielektrischen und Leitungsverluste sind schwer zu berechnen und werden daher oft gemessen. Auch bei Messungen ist die Trennung schwierig. Die kombinierten Verluste bilden die Strahlungswirkungsgrad(ecd). Die Definition der Strahlungswirkungsgrad ist das Verhältnis der abgegebenen Leistung zum Strahlungswiderstand (Rr) zu der an den Strahlungswiderstand abgegebenen Leistung und dem Leitungs-Dielektrikum-Widerstand (RL).
- Ecd = Strahlungswirkungsgrad der Antenne
- Rr = Strahlungswiderstand
- RL = Widerstand, der die Kombination der Leitungs-Dielektrikum-Verluste darstellt
Antennentemperatur-Rechner
Jedes Objekt mit einer physischen Temperatur über dem absoluten Nullpunkt strahlt Energie aus. Die äquivalente Temperatur stellt die Menge der abgestrahlten Energie dar.
Wenn eine Antenne, die auf einer bestimmten physikalischen Temperatur (Tp) gehalten wird, über eine Länge der Übertragungsleitung (L) mit einer konstanten Temperatur (To) an einen Empfänger angeschlossen ist und eine gleichmäßige Dämpfung (α) aufweist, kann die effektive Antennentemperatur am Empfangsgerät Tant unter Berücksichtigung der physischen Temperatur TAP berechnet werden.
Die in der Gleichung verwendeten Parameter sind:
- Tant = Antennentemperatur am Empfangsgerät (K)
- TA = Antennenrauschtemperatur an den Antennenanschlüssen (K)
- TAP = Antennentemperatur an den Antennenanschlüssen aufgrund der physischen Temperatur (K)
- Tp = physikalische Temperatur der Antenne (K)
- α = Dämpfungskoeffizient der Übertragungsleitung (Np/m)
- εA = Wärmewirkungsgrad der Antenne
- L = Länge der Übertragungsleitung (m)
- To = physikalische Temperatur der Übertragungsleitung (K)
Rechner für realisierten Antennengewinn
Der realisierte Gewinn einer Antenne wird unter Berücksichtigung des Gesamtwirkungsgrads der Antenne zusammen mit ihrer Richtwirkung berechnet.
Die Gesamteffizienz der Antenne berücksichtigt die Verluste aufgrund von Reflexionen an den Eingangsanschlüssen und Verluste innerhalb der Struktur der Antenne.
Die Gesamteffizienz e0 kann wie folgt geschrieben werden:
Dabei ist er die Reflexionseffizienz (Diskrepanz), ed die Dielektrikum-Effizienz und ec die Leitungseffizienz. Die Dielektrikums- und Leitungseffizienzen werden in der Regel gruppiert, da sie als eine Einheit gemessen werden, und als ecd bezeichnet. Wir können die Gesamteffizienz wie folgt schreiben:
Wir berechnen die realisierte Verstärkung unter Verwendung der Gesamteffizienz und der Richtwirkung wie folgt:
Die realisierte Verstärkung und Richtwirkung werden in dBi angegeben, der Spannungsreflexionskoeffizient in dB und der Wirkungsgrad als Wert zwischen 0 und 1.
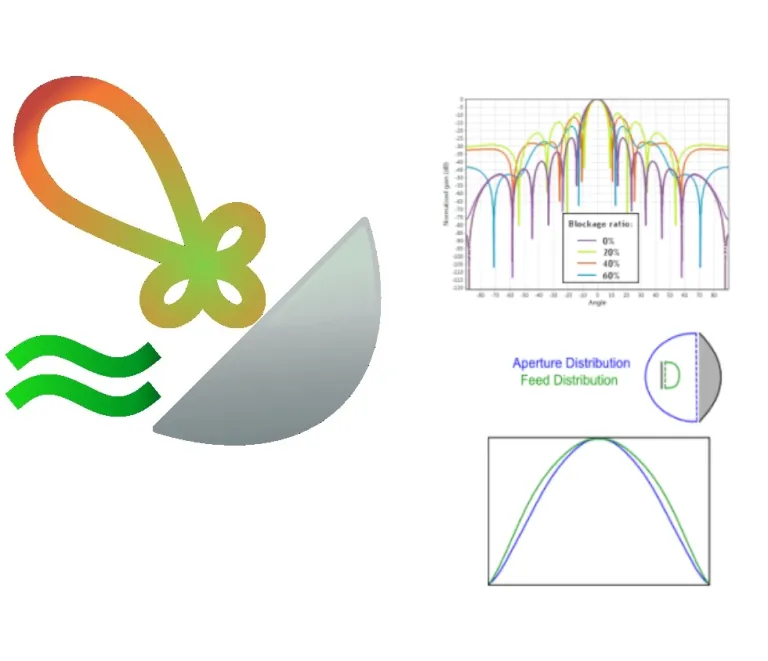
Rechner für die Aperturverteilung
Dieser Rechner stellt die ungefähre Apertur und die Speisungsverteilung einer typischen achsensymmetrischen Parabolreflektortopologie dar. Die Speisungs-/Aperturverteilung wird auf Grundlage folgender Werte bestimmt:
- Formmodifikator (P), abgeleitet für die gegebene Brennweite auf
- Durchmesserverhältnis (F/D),
- Kantenverjüngung (ET) und
- Apertur-/Speisungsverteilungseffizienz (ade / f de) [Rahmat-Samii].
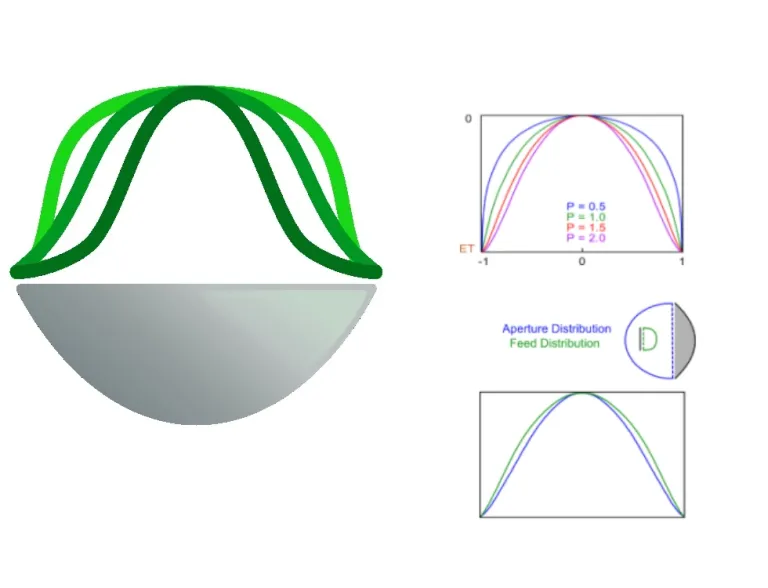
Diese Abbildung zeigt den Effekt des Formmodifikators P auf die Speisungs-/Aperturverteilung:
Die Verteilung an der Versorgung unterscheidet sich aufgrund der Eigenschaften des Hauptreflektors von der Speisung an der Apertur. Das Diagramm hängt vom F/D-Verhältnis der Schüssel ab. Die Apertur- oder Speisungseffizienz wird relativ zu einer „idealen“ flachen Verteilung berechnet.
Tool für Richtdiagramm-Approximation
Für eine bestimmte Parabolreflektorschüssel und Speisungsantenne berechnen wir das Strahungsdiagram mit dem praktischen Tool für die Diagramapproximation. Mit diesem Tool kann der Benutzer den theoretischen Antennengewinn und das Strahlungsdiagramm größerer Reflektoren berücksichtigen, was zu langen Simulationszeiten führen kann. Es ermöglicht auch die Vorhersage des Einflusses von Parametern wie Blockierungsverhältnis oder Effizienz der Versorgungsverteilung.
Beispielsweise lassen sich mit dem Tool ganz ohne Simulation die Auswirkungen des Blockierungsverhältnisses auf die Richtcharakteristik untersuchen, wie in der Grafik dargestellt.
Dabei werden die folgenden Parameter konstant gehalten:
- Betriebsfrequenz: 10 GHz
- D (Reflektordurchmesser): 200 mm
- F/D-Verhältnis: 0,34
- ET (Kantenverjüngung): -35 dB
- Fde (Speisungsverteilungseffizienz): 70 %
Die Verteilung an der Versorgung unterscheidet sich aufgrund der Eigenschaften des Hauptreflektors von der Speisung an der Apertur. Das Diagramm hängt vom F/D-Verhältnis der Schüssel ab. Die Apertur- oder Speisungseffizienz wird relativ zu einer „idealen“ flachen Verteilung berechnet.
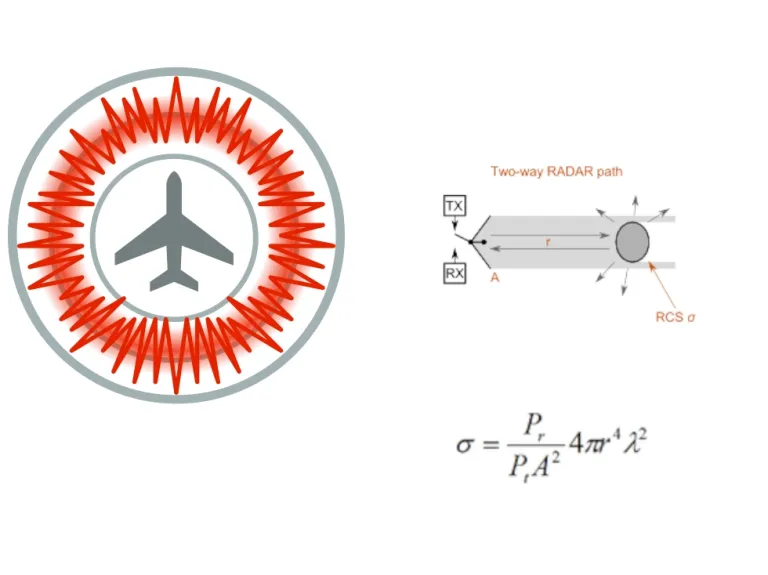
Radarquerschnittrechner
Der Radarquerschnitt (Radar Cross Section, RCS) eines Objekts ist dessen effektiver Bereich, der die einfallende Leistungsdichte abfängt, was bei isotropischer Streuung zu der empfangenen Rückstreuungsleistung führen würde. Bei der Schätzung wird davon ausgegangen, dass die Polarisationen übereinstimmen.
Dieser Rechner gibt den Radarquerschnitt (Radar Cross Section, RCS) eines Objekts unter Berücksichtigung verschiedener Eingabeziele zurück.
Die vereinfachte Gleichung in diesem Rechner bestimmt das RCS eines Objekts anhand der Frequenz, der empfangenen Leistung, der übertragenen Leistung, des Gesamtpfadabstands und der Antennenaperturfläche.
Eine Antenne ist ein Objekt mit einem eindeutigen RCS-Merkmal, da ein Teil der empfangenen Leistung an die Antennenanschlüsse geliefert wird. Eine gute Impedanzanpassung an das Signal reduziert die Rückstrahlung und somit den RCS.
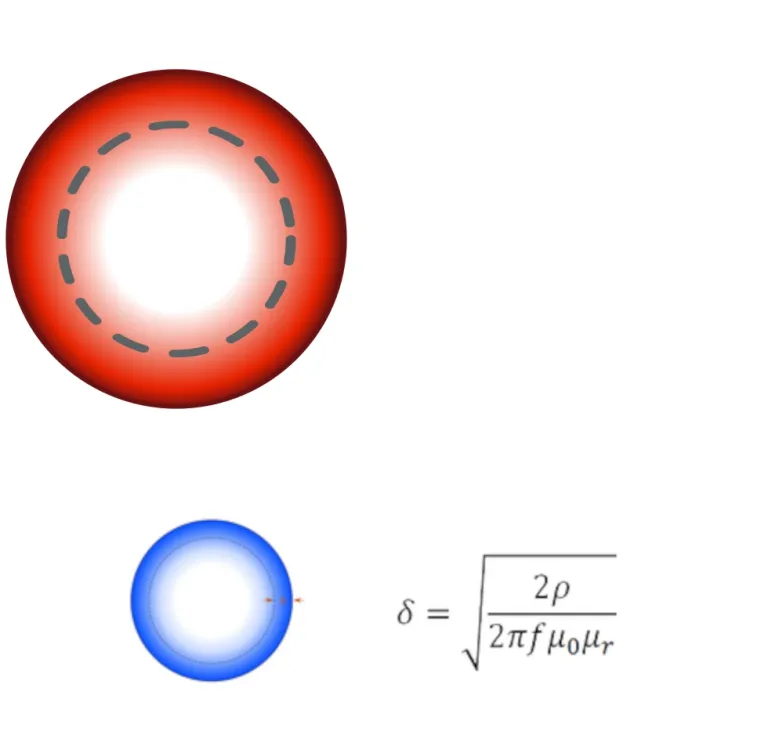
Rechner für äquivalente Leitschichtdicke
Die äquivalente Leitschichtdicke ist ein Maß für die elektrische Leitfähigkeit innerhalb eines Leiters. Bei Gleichstrom (0 Hz) wird der Strom gleichmäßig über den Querschnitt eines Leiters verteilt. Mit zunehmender Frequenz ändert sich die Stromverteilung mit der höchsten Stromdichte nahe der Leiteroberfläche.
Die äquivalente Leitschichtdicke δ ist eine Funktion aus Frequenz, relativer Permeabilität des Leiters, μr, und Widerstand, ρ (oder Leitfähigkeit, ο, wobei ο = 1/ ρ). Sie ist definiert als die Tiefe unterhalb der Oberfläche eines Leiters, bei der die Stromdichte auf 1/e (≈ 0,37) der Stromdichte an der Oberfläche gefallen ist.
Dabei gilt Folgendes:
δ: Äquivalente Leitschichtdicke [m]
μ0: Vakuumdurchlässigkeit [H.m-1]
ρ: Widerstand [Ω.m]
ο: Leitfähigkeit [S.m-1]
Entdecken Sie auch
Erfahren Sie, was SIMULIA für Sie tun kann
Lassen Sie sich von unseren SIMULIA Experten zeigen, wie unsere Lösungen eine nahtlose Zusammenarbeit und nachhaltige Innovation in Unternehmen jeder Größe ermöglichen.
Erste Schritte
Wir bieten Kurse und Schulungen für Studenten, Hochschulen, Fachleute und Unternehmen an. Finden Sie die passende SIMULIA Schulung.
Hilfe anfordern
Informationen zu Software- und Hardware-Zertifizierungen, Software-Downloads, Anwenderdokumentation, Support-Kontakten und Serviceangeboten finden