Automatische Optimierung
CST Studio Suite bietet automatische Optimierungsroutinen für elektromagnetische Systeme und Geräte
Parametrisierung und Optimierung mit CST Studio Suite
Parametrierung von Simulationsmodellen
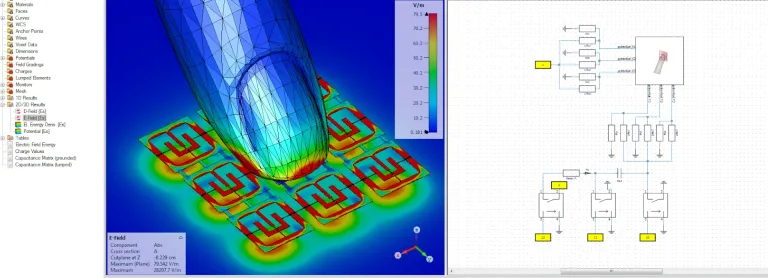
CST Studio Suite Modelle können hinsichtlich ihrer geometrischen Abmessungen oder Materialeigenschaften parametrisiert werden. Sie können Parameter jederzeit einführen, während des Modellierungsprozesses oder nachträglich. Anwender können über die Benutzeroberfläche auf ihre Parametrierung zugreifen, um das Verhalten eines Geräts zu beobachten, wenn sich seine Eigenschaften ändern.
Parameterstudien und automatische Optimierung
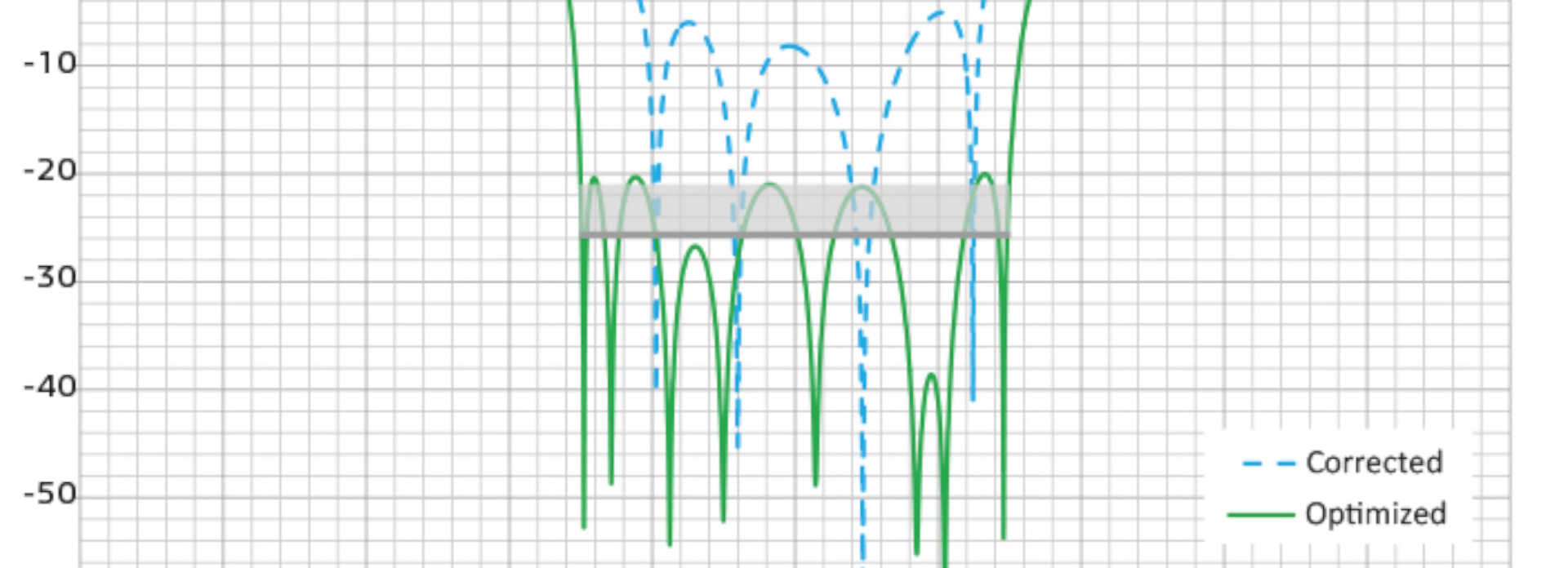
Mit einer Parameterstudie können Anwender die optimalen Konstruktionsparameter finden, um einen bestimmten Effekt oder ein bestimmtes Ziel zu erreichen. Sie können auch Materialeigenschaften anpassen, um Materialmodelle mit gemessenen Daten abzugleichen.
CST Studio Suite enthält mehrere automatische Optimierungsalgorithmen, sowohl lokale als auch globale. Lokale Optimierer ermöglichen eine schnelle Konvergenz, laufen jedoch Gefahr, gegen ein lokales Minimum zu konvergieren, statt die beste Gesamtlösung zu finden. Globale Optimierer hingegen durchsuchen den gesamten Problembereich, erfordern aber in der Regel umfassendere Berechnungen.
Beschleunigung des Optimierungsprozesses
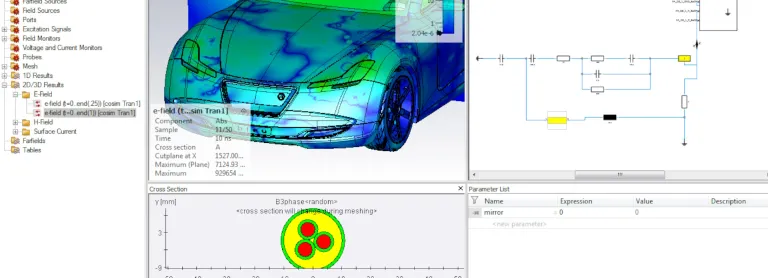
Die für eine Optimierung benötigte Zeit hängt von der Lösungszeit für eine einzelne elektromagnetische Simulation sowie von der Anzahl der Iterationen ab, die erforderlich sind, um zur optimalen Lösung zu gelangen. Leistungsstarke Rechenverfahren können eingesetzt werden, um die Simulation und Optimierung für sehr komplexe Systeme oder Probleme mit einer großen Anzahl von Variablen zu beschleunigen.
Die Gesamtleistung von globalen Optimierern und unabhängigen Parameterstudien profitiert von der Möglichkeit, einzelne Sätze parallel auszuführen. Die verteilte Berechnung kann die Leistung für diese Anwendungen erheblich verbessern.
CST Studio Suite Optimierer
Entdecken Sie auch
Erfahren Sie, was SIMULIA für Sie tun kann
Lassen Sie sich von unseren SIMULIA Experten zeigen, wie unsere Lösungen eine nahtlose Zusammenarbeit und nachhaltige Innovation in Unternehmen jeder Größe ermöglichen.
Erste Schritte
Wir bieten Kurse und Schulungen für Studenten, Hochschulen, Fachleute und Unternehmen an. Finden Sie die passende SIMULIA Schulung.
Hilfe anfordern
Informationen zu Software- und Hardware-Zertifizierungen, Software-Downloads, Anwenderdokumentation, Support-Kontakten und Serviceangeboten finden