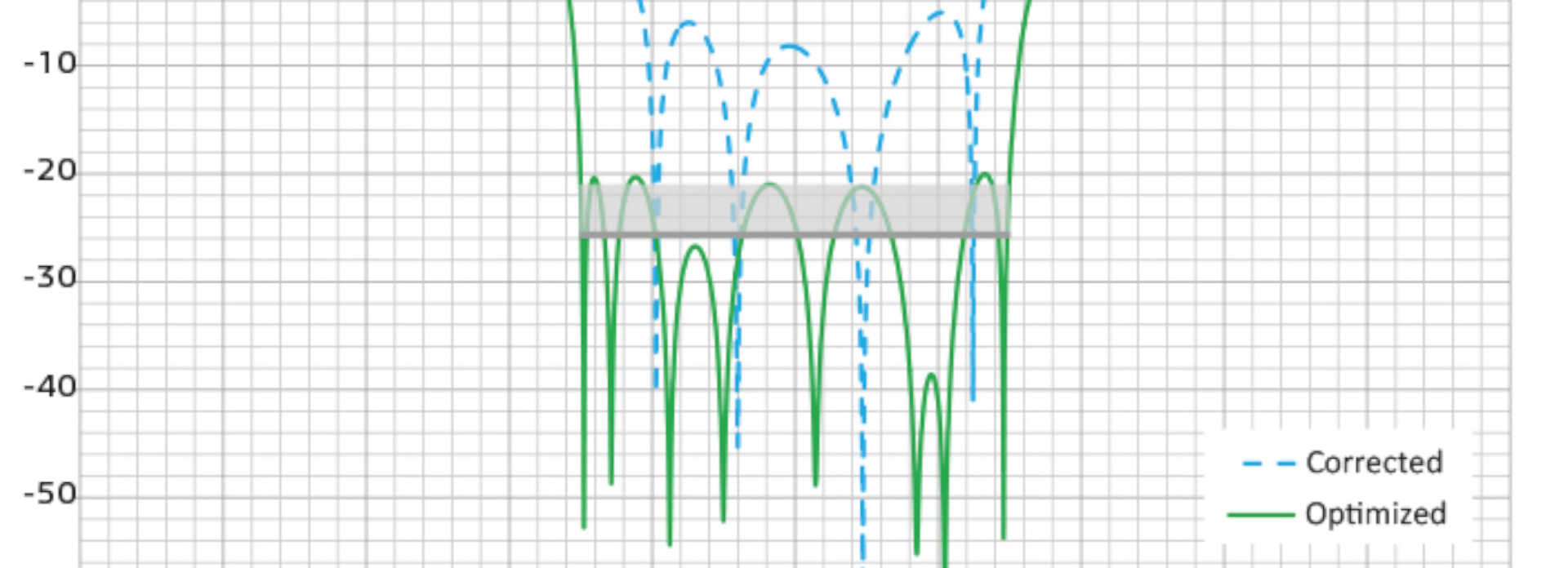
Automatische Optimierung
CST Studio Suite bietet automatische Optimierungsroutinen für elektromagnetische Systeme und Geräte
Parametrisierung und Optimierung mit CST Studio Suite
Parametrierung von Simulationsmodellen
CST Studio Suite Modelle können hinsichtlich ihrer geometrischen Abmessungen oder Materialeigenschaften parametrisiert werden. Sie können Parameter jederzeit einführen, während des Modellierungsprozesses oder nachträglich. Anwender können über die Benutzeroberfläche auf ihre Parametrierung zugreifen, um das Verhalten eines Geräts zu beobachten, wenn sich seine Eigenschaften ändern.
Parameterstudien und automatische Optimierung
Mit einer Parameterstudie können Anwender die optimalen Konstruktionsparameter finden, um einen bestimmten Effekt oder ein bestimmtes Ziel zu erreichen. Sie können auch Materialeigenschaften anpassen, um Materialmodelle mit gemessenen Daten abzugleichen.
CST Studio Suite enthält mehrere automatische Optimierungsalgorithmen, sowohl lokale als auch globale. Lokale Optimierer ermöglichen eine schnelle Konvergenz, laufen jedoch Gefahr, gegen ein lokales Minimum zu konvergieren, statt die beste Gesamtlösung zu finden. Globale Optimierer hingegen durchsuchen den gesamten Problembereich, erfordern aber in der Regel umfassendere Berechnungen.
Beschleunigung des Optimierungsprozesses
Die für eine Optimierung benötigte Zeit hängt von der Lösungszeit für eine einzelne elektromagnetische Simulation sowie von der Anzahl der Iterationen ab, die erforderlich sind, um zur optimalen Lösung zu gelangen. Leistungsstarke Rechenverfahren können eingesetzt werden, um die Simulation und Optimierung für sehr komplexe Systeme oder Probleme mit einer großen Anzahl von Variablen zu beschleunigen.
Die Gesamtleistung von globalen Optimierern und unabhängigen Parameterstudien profitiert von der Möglichkeit, einzelne Sätze parallel auszuführen. Die verteilte Berechnung kann die Leistung für diese Anwendungen erheblich verbessern.
CST Studio Suite Optimierer
Die Kovarianz-Matrix-Adaptations-Evolutionsstrategie (Covariance Matrix Adaptation Evolutionary Strategy, kurz CMA-ES) ist der am weitesten entwickelte globale Optimierer und weist eine für einen globalen Optimierer relativ schnelle Konvergenz auf. Bei CMA-ES kann sich der Optimierer frühere Iterationen „merken“. Dadurch lassen sich nicht nur die Leistung des Algorithmus verbessern, sondern auch lokale Optima vermeiden.
Geeignet für: Allgemeine Optimierung, insbesondere bei komplexen Problembereichen
Ein leistungsstarker lokaler Optimierer, der basierend auf Primärdaten ein lineares Modell in einem „vertrauenswürdigen“ Bereich um den Ausgangspunkt herum aufbaut. Die modellierte Lösung wird als neuer Ausgangspunkt verwendet, bis sie zu einem akkuraten Datenmodell konvergiert. Das Trust-Region-Framework nutzt S-Parameter-Sensitivitätsinformationen, um die Anzahl der erforderlichen Simulationen zu reduzieren und den Optimierungsprozess zu beschleunigen. Es ist der robusteste Optimierungsalgorithmus.
Geeignet für: Allgemeine Optimierung, insbesondere bei Modellen mit Sensitivitätsinformationen
Mithilfe eines evolutionären Optimierungsansatzes generiert der genetische Algorithmus Punkte im Parameterraum und verfeinert diese dann über mehrere Generationen durch zufällige Parameteränderung. Durch die Auswahl der „passendsten“ Parametersätze einer jeden Generation konvergiert der Algorithmus zu einem globalen Optimum.
Geeignet für: Komplexe Problembereiche und Modelle mit vielen Parametern
Dieser Algorithmus gehört ebenfalls zu den globalen Optimierern. Er behandelt Punkte im Parameterbereich als bewegliche Teilchen. Bei jeder Iteration ändert sich die Partikelposition nicht nur abhängig von der besten bekannten Position eines jeden Partikels, sondern auch in Abhängigkeit der besten Position des gesamten Partikelschwarms. Die Partikelschwarmoptimierung eignet sich gut für Modelle mit vielen Parametern.
Geeignet für: Modelle mit vielen Parametern
Hierbei handelt es sich um eine lokale Optimierungsmethode, bei der anhand mehrerer über den Parameterbereich verteilter Punkte das Optimum ermittelt wird. Der Nelder-Mead-Simplex-Algorithmus ist weniger abhängig vom Ausgangspunkt als die meisten lokalen Optimierer.
Geeignet für: Komplexe Problembereiche mit relativ wenigen Parametern; Systeme ohne gutes Anfangsmodell
Der interpolierte Quasi-Newton-Optimierer ist ein schneller lokaler Optimierer, der sich mittels Interpolation dem Gradienten des Parameterraums annähert. Das interpolierte Quasi-Newton-Verfahren weist eine schnelle Konvergenz auf.
Geeignet für: Rechenintensive Modelle
Der klassische Powell-Optimierer ist ein einfacher, robuster lokaler Optimierer für Einzelparameter-Probleme. Obwohl er langsamer ist als das interpolierte Quasi-Newton-Verfahren, übertrifft er dieses zuweilen bei der Genauigkeit.
Geeignet für: Optimierung mit einer Variablen
Der Decap-Optimierer ist ein spezieller Optimierer für Leiterplatten. Er berechnet die effektivste Platzierung von Entkopplungskondensatoren mithilfe des Pareto-Optimums. Der Optimierer hilft, entweder die Anzahl der benötigten Kondensatoren oder die Gesamtkosten zu senken und dennoch die angegebene Impedanzkurve zu erreichen.
Geeignet für: PCB-Layout
Entdecken Sie auch
Erfahren Sie, was SIMULIA für Sie tun kann
Lassen Sie sich von unseren SIMULIA Experten zeigen, wie unsere Lösungen eine nahtlose Zusammenarbeit und nachhaltige Innovation in Unternehmen jeder Größe ermöglichen.
Erste Schritte
Wir bieten Kurse und Schulungen für Studenten, Hochschulen, Fachleute und Unternehmen an. Finden Sie die passende SIMULIA Schulung.
Hilfe anfordern
Informationen zu Software- und Hardware-Zertifizierungen, Software-Downloads, Anwenderdokumentation, Support-Kontakten und Serviceangeboten finden