SIMULIA
Reveal the World We Live In
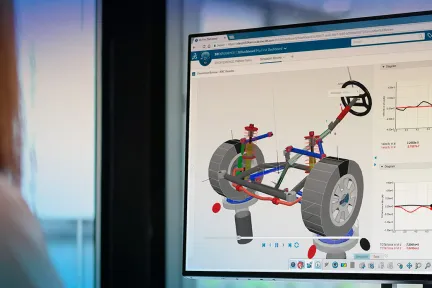
SIMULIA 시뮬레이션 소프트웨어는 물리적인 시제품을 제작하기 전에 재료와 제품의 성능, 신뢰성, 안전성을 평가하는 프로세스를 가속화합니다. 다쏘시스템에서 지원하는 엔지니어링 분야를 살펴보세요.
기계 및 토목 엔지니어링을 위한 유한 요소 해석
전자기장 시뮬레이션 및 해석
고체 및 구조물 주변의 정상 상태 및 과도 상태 내외부 유동
기계적 힘을 적용한 복잡한 기계 시스템의 모션 해석
전체 가청 주파수 범위에서 소음 및 진동의 시뮬레이션 및 해석
시뮬레이션을 대중화하고, 혁신을 가속화하며, 인공지능의 힘을 활용하세요.
SIMULIA 포트폴리오
소프트웨어와 솔루션 살펴보기
주요 주제
SIMULIA의 세계를 만나보세요
3DEXPERIENCE 플랫폼의 모델링 및 시뮬레이션
AI 기반 성능 중심 설계와 머신러닝을 통해 시뮬레이션에서 더 많은 가치를 창출하고 업무 효율성을 높이세요.
클라우드 시뮬레이션을 통해 미래를 밝히다
커넥티드 시스템 및 장치의 시뮬레이션을 통한 효율적인 제품 설계 및 인증
SIMULIA의 Advanced Digital Additive Manufacturing Solutions를 통해 제작의 미래에 대해 알아보세요
시뮬레이션은 EV 설계를 최적화하고 성능을 향상시키며 지속 가능한 운송수단의 미래를 만듭니다.
도심 항공 모빌리티(UAM)를 위한 시뮬레이션
고객 사례
기업에서 설계 및 엔지니어링 시뮬레이션 솔루션을 사용하는 방법
Helix
차세대 전동 파워트레인
전동 파워트레인 개발사인 Helix는 고성능 전기 모터와 인버터로 기록을 경신하고 상을 수상했습니다. 지속적인 개선을 추진하며 3DEXPERIENCE를 통해 미세하게 조정된 설계를 완성하고 개념부터 제조에 이르는 엔지니어링 프로세스를 간소화하고 있습니다.
3DEXPERIENCE는 설계 및 생산까지 우리가 하는 모든 일의 중심에 있습니다.
이벤트
e세미나
사용자 커뮤니티
필수 SIMULIA 리소스 제공 및 동료 사용자와의 적극적인 교류
SIMULIA 챔피언 프로그램
SIMULIA 챔피언 프로그램은 가장 적극적으로 활동하고 영향력이 큰 시뮬레이션 전문가들이 한 곳에 모여 시뮬레이션의 미래를 발전시킬 수 있도록 도와줍니다.
우리의 챔피언은 다른 사용자와 탁월한 전문 지식을 공유하고, 동료들에게 영감을 주고, 중요한 피드백을 제공하며, SIMULIA 커뮤니티를 풍요롭게 하는 브랜드 홍보대사입니다.
블로그
SIMULIA 블로그에서 당사 전문가들이 전하는 최신 뉴스와 혁신에 대해 알아보세요.
eBook, 백서, 기타 리소스
SIMULIA와 연결
SIMULIA의 지원 서비스 알아보기
SIMULIA 전문가와 상담하여 당사의 솔루션이 모든 규모의 조직에서 원활한 협업과 지속 가능한 혁신을 실현하는 방법에 대해 알아보세요.
시작하기
학생, 교육, 전문가 및 회사를 위한 교육 과정과 강의가 제공됩니다. 당신에게 맞는 SIMULIA 교육을 찾아보세요.
도움받기
소프트웨어 및 하드웨어 인증, 소프트웨어 다운로드, 사용자 설명서, 지원 연락처 및 서비스 제공에 대한 정보를 확인하세요.