Optimisation automatique
Utiliser des routines d'optimisation automatiques destinées aux équipements et systèmes électromagnétiques avec CST Studio Suite
Paramétrage et optimisation avec CST Studio Suite
Paramétrage des modèles de simulation
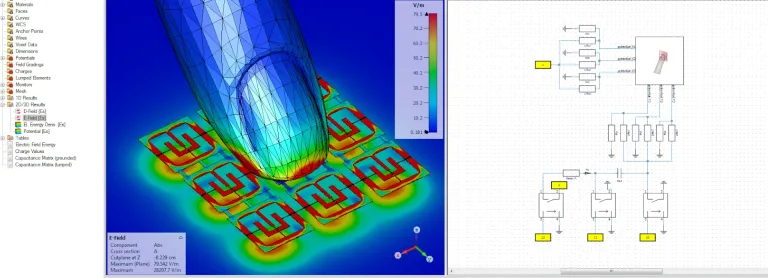
Les modèles CST Studio Suite peuvent être paramétrés en fonction de leurs cotes géométriques ou des propriétés des matériaux. Vous pouvez introduire des paramètres à tout moment, pendant le processus de modélisation ou de manière rétrospective. Les utilisateurs peuvent accéder à leur paramétrage via l'interface pour étudier le comportement d'un appareil à mesure que ses propriétés changent.
Études paramétriques et optimisation automatique
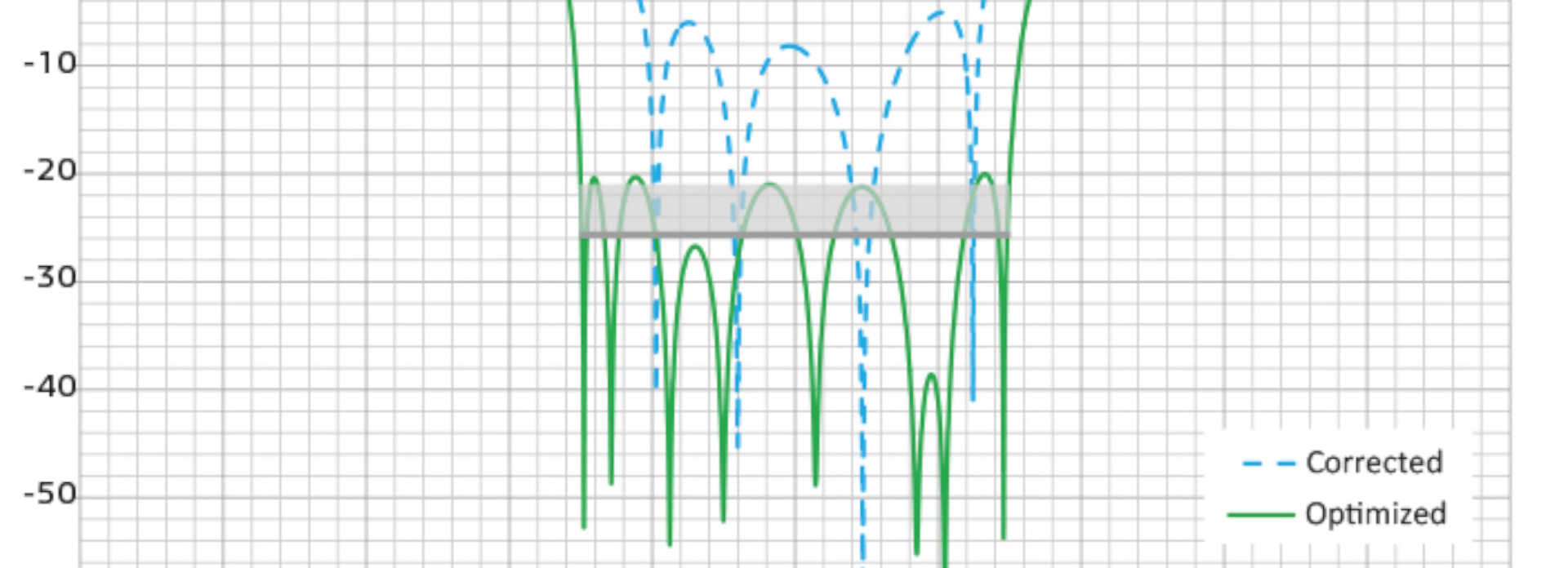
Grâce à l'étude paramétrique, les utilisateurs peuvent identifier les paramètres de conception optimaux afin d'obtenir l'effet souhaité ou d'atteindre l'objectif fixé. Ils peuvent également adapter les propriétés des matériaux pour que les modèles correspondent aux données mesurées.
CST Studio Suite contient plusieurs algorithmes d'optimisation automatique à l'échelle locale et globale. Les optimiseurs locaux fournissent une convergence rapide mais locale, plutôt qu'une solution globale de meilleure qualité. D'un autre côté, les optimiseurs globaux effectuent des recherches sur la totalité de l'espace du problème, ce qui exige plus de calculs.
Optimisation plus rapide
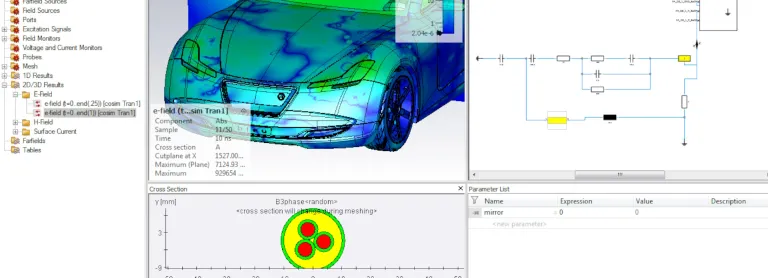
Le temps requis pour une optimisation dépend du délai de résolution de chaque simulation électromagnétique, mais aussi du nombre d'itérations requises pour parvenir à la solution optimale. Il est possible d'utiliser des techniques de calcul haute performance pour faciliter la simulation et l'optimisation de systèmes très complexes ou de problèmes présentant de nombreuses variables.
Les optimiseurs globaux et les études paramétriques indépendantes offrent de meilleures performances lorsqu'il est possible d'exécuter des ensembles distincts en parallèle. L'informatique distribuée peut considérablement améliorer les performances de ces applications.
Optimiseurs CST Studio Suite
L'optimiseur Stratégie évolutionnaire d'adaptation de la matrice de covariance (CMA-ES) est le plus sophistiqué des optimiseurs globaux. Il dispose d'une convergence relativement rapide pour un optimiseur global. Grâce à la stratégie évolutionnaire d'adaptation de la matrice de covariance, l'optimiseur peut se « souvenir » des itérations précédentes, ce qui permet d'améliorer les performances de l'algorithme tout en évitant les optimums locaux.
Convient pour : optimisation générale, notamment pour les domaines à problèmes complexes
Un optimiseur local puissant qui construit un modèle linéaire sur des données primaires dans une région « de confiance » près du point de départ. Il utilise la solution modélisée comme nouveau point de départ jusqu'à ce qu'il converge vers un modèle précis des données. La structure de région de confiance tire parti des informations de sensibilité du paramètre S pour réduire le nombre de simulations requises et raccourcir le processus d'optimisation. C'est l'algorithme d'optimisation le plus robuste.
Convient pour : optimisation générale, notamment sur les modèles intégrant des informations de sensibilité
S'appuyant sur une approche évolutionnaire de l'optimisation, l'algorithme génétique génère des points dans l'espace des paramètres, puis les affine suivant plusieurs générations avec une mutation des paramètres aléatoire. En sélectionnant les ensembles de paramètres les plus « adéquats » de chaque génération, l'algorithme converge vers un optimum global.
Convient pour : domaines à problèmes complexes et modèles avec de nombreux paramètres
Cet algorithme est un autre optimiseur global qui traite les points se trouvant dans l'espace des paramètres comme des particules en mouvement. À chaque itération, la position des particules change en fonction de la meilleure position connue de chaque particule, mais également de la meilleure position de tout l'essaim. L'optimisation par essaim de particules fonctionne bien pour les modèles disposant de nombreux paramètres.
Convient pour : modèles avec de nombreux paramètres
Cette méthode est une technique d'optimisation locale qui utilise différents points répartis dans l'espace des paramètres pour trouver l'optimum. L'algorithme à simplexe Nelder-Mead est moins dépendant du point de départ que la plupart des optimiseurs locaux.
Convient pour : domaines à problèmes complexes ayant relativement peu de paramètres ou systèmes sans modèle de base approprié
L'optimiseur interpolé quasi-Newton est un optimiseur local qui utilise l'interpolation pour donner une approximation du gradient de l'espace des paramètres. La méthode interpolée quasi-Newton offre une convergence rapide.
Convient pour : modèles exigeant de nombreux calculs
L'optimiseur Powell classique est un optimiseur local simple et robuste pour les problèmes à un seul paramètre. Bien qu'il soit plus lent que l'optimiseur interpolé quasi-Newton, il peut parfois être plus précis.
Convient pour : optimisation à une seule variable
L'optimiseur de condensateur de découplage (Decap Optimizer) est spécialisé dans la conception de cartes à circuits imprimés. Il calcule le placement le plus efficace des condensateurs de découplage en utilisant préalablement le principe de Pareto. Il permet de réduire au minimum le nombre de condensateurs requis ou le coût total tout en respectant la courbe d'impédance spécifiée.
Convient pour : agencement de cartes de circuits imprimés
À découvrir également
Logiciel de simulation de champ électromagnétique
Tirer parti des solveurs de simulation CST Studio Suite pour les systèmes et appareils électromagnétiques
Utiliser une interface utilisateur graphique pour les systèmes et appareils électromagnétiques avec CST Studio Suite
Simplifier la gestion des projets de simulation grâce à l'environnement CST Studio Suite
Options d'importation et d'échange de données de CST Studio Suite pour rationaliser la conception électromagnétique
Découvrir comment SIMULIA peut vous aider
Contactez un expert SIMULIA pour découvrir comment nos solutions permettent une collaboration transparente et une innovation durable dans des entreprises de toutes tailles.
Commencer
Des formations et des cours sont disponibles pour les étudiants, le monde académique, les professionnels et les entreprises. Trouvez la formation SIMULIA qui vous convient.
Obtenir de l'aide
Obtenez des informations sur la certification des logiciels et du matériel, les téléchargements de logiciels, la documentation utilisateur, les coordonnées du support et l'offre de services.